Как Найти Функцию Кривой

Как найти функцию кривой?

Поиск функции кривой является задачей, которая может иметь различные подходы и методы в зависимости от предоставленных данных и условий задачи. Вот несколько шагов, которые могут помочь вам в этом процессе:

1. Сбор данных: Начните собирать информацию о кривой, для которой вы хотите найти функцию. Это может включать точки, через которые проходит кривая, значения особых точек (например, вершины, точки перегиба) или любую другую доступную информацию.

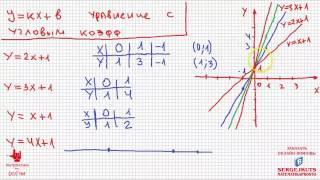
2. Анализ типа кривой: Определите тип кривой, с которой вы работаете. Например, это может быть парабола, синусоида, гипербола и т. д. Знание типа кривой может помочь сужать диапазон возможных функций.

3. Рассмотрение общего вида функции: Исследуйте, какими свойствами должна обладать функция, чтобы соответствовать кривой. Например, угол наклона, симметрия, асимптотическое поведение и так далее.

4. Разработка гипотезы: На основе анализа данных и типа кривой сформулируйте гипотезы о возможной функции, которая описывает данную кривую. Обычно это будет уравнение, включающее переменные и коэффициенты.

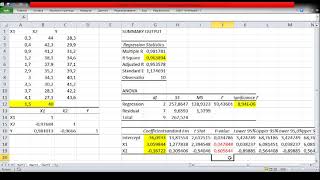
5. Настройка и проверка гипотезы: Используйте полученные данные и условия задачи, чтобы определить значения переменных и коэффициентов в гипотезе. После этого проверьте, соответствуют ли предсказанные значения ожидаемым данным. Если нет, то можно модифицировать гипотезу и продолжить итерационный процесс.

6. Проверка решения: После того как вы найдете функцию, которая наилучшим образом описывает кривую, проверьте ее на других точках или условиях, чтобы удостовериться в ее точности.

Важно понимать, что процесс поиска функции кривой может быть сложным и требовать глубокого знания математики и аналитической геометрии. В случае затруднений или неопределенности всегда рекомендуется обратиться к опытным специалистам или исследователям, которые могут помочь в решении данной задачи.