КАК ДОКАЗАТЬ ТЕОРЕМУ СИНУСОВ 9 КЛАСС
Как доказать теорему синусов в 9-м классе?
Для доказательства теоремы синусов в 9-м классе можно использовать геометрический подход и аналитическую геометрию.
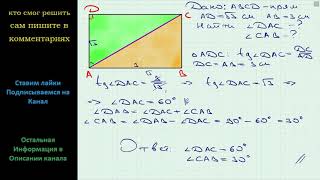
Геометрический подход заключается в построении треугольника и использовании соответствующих геометрических отношений. Нам необходимо взять треугольник со сторонами a, b и c, где a и b - это две стороны треугольника, а c - гипотенуза.
Далее, мы можем использовать определение синуса треугольника, которое гласит: синус угла треугольника равен отношению противолежащей стороны к гипотенузе. Мы получим следующее уравнение: sin(A) = a/c и sin(B) = b/c, где A и B - это углы треугольника.
Аналитический подход использует координаты точек треугольника на плоскости. Мы можем выбрать треугольник на координатной плоскости и задать координаты вершин треугольника. Затем, используя формулу расстояния между двумя точками, мы можем найти длины сторон треугольника.
Далее, мы можем использовать формулу синуса, которая гласит: sin(A) = |BC| / |AC| и sin(B) = |AC| / |BC|, где |BC| и |AC| - это длины сторон треугольника.
Таким образом, используя геометрический подход или аналитический подход, мы можем доказать теорему синусов в 9-м классе.
Как быстро и легко выучить теорему по математике. На примере теоремы Пифагора
9 класс, 13 урок, Теорема синусов
ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия - Математика
Теорема синусов – просто и красиво // Vital Math
Теорема синусов и теорема косинусов
ЛУЧШЕЕ ДОКАЗАТЕЛЬСТВО теоремы Синусов
Теорема о трёх перпендикулярах - Ботай со мной #032 - Борис Трушин -
Теорема синусов с доказательством
Теоремы синусов и косинусов - Ботай со мной #029 - Борис Трушин