КАК НАЙТИ ЭКСТРЕМУМЫ ФУНКЦИИ ПРИМЕРЫ ЧЕРЕЗ ПРОИЗВОДНУЮ
Экстремумы функции являются точками, в которых функция достигает своих наибольших или наименьших значений на заданном промежутке. Чтобы найти экстремумы функции, можно использовать производную.
Для начала необходимо найти производную функции с помощью правил дифференцирования, таких как правило степени, правило произведения или правило сложной функции.
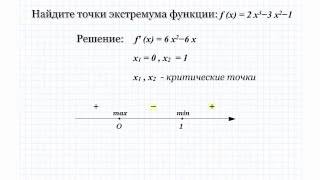
Затем найденную производную необходимо приравнять к нулю и решить полученное уравнение относительно переменной. Полученные значения переменной являются кандидатами на экстремумы функции.
Далее нужно проверить значения производной на предмет изменения знака в окрестности каждой кандидатской точки. Если производная меняет знак с плюса на минус, то в данной точке функция достигает локального максимума, а если производная меняет знак с минуса на плюс, то функция достигает локального минимума. В случае если знак производной не меняется, то в данной точке нет локального экстремума.
Например, рассмотрим функцию f(x) = x^2. Найдем ее производную: f'(x) = 2x. Приравняем ее к нулю: 2x = 0. Решим уравнение и получим x = 0. Значит, точка x = 0 является кандидатом на экстремум. Теперь проверим значения производной в окрестности точки x = 0. При x < 0 производная отрицательна, а при x > 0 производная положительна. Значит, в точке x = 0 функция достигает локального минимума.
10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумы
Математический анализ, 12 урок, Монотонность и экстремумы функции
Производная: секретные методы решения. Готовимся к ЕГЭ - Математика TutorOnline
Исследование функции на монотонность и экстремумы
Найти точки экстремума функции
Математика без Ху%!ни. Экстремум функции 2х переменных.
4. Вычисление производных примеры. Самое начало.
АЛГЕБРА С НУЛЯ — Точки Экстремума Функции