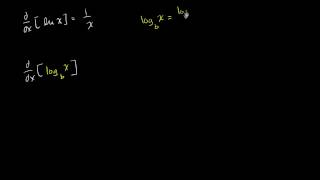КАК РЕШАТЬ ЛОГАРИФМЫ LG
Логарифмы являются важным понятием в математике и широко используются в программировании и алгоритмах. Логарифм по основанию 10 (обычно обозначается как lg) – это обратная функция к операции возведения числа в степень. Решение логарифма lg включает в себя нахождение такого числа, при возведении которого в указанную степень получится заданное число.
Чтобы решить логарифм lg, необходимо использовать свойства логарифмов и алгоритмы для расчетов. Важным свойством логарифма является изменение основания логарифма при переходе к другому основанию. Для примера, логарифм по основанию 10 (lg) может быть преобразован в логарифм по основанию 2 (логарифм по основанию 2 обозначается как log2) с помощью следующей формулы: log2(x) = lg(x) / lg(2).
Для решения логарифма lg можно использовать различные методы, такие как графический метод, табличный метод или метод с помощью калькулятора. Для графического метода необходимо построить график функции, содержащей логарифмическое выражение, и определить точку пересечения этой функции с заданной прямой. Табличный метод предполагает составление таблицы значений, где каждому значению известного логарифма соответствует значение аргумента. Используя калькулятор, можно найти решение логарифма, вводя его аргумент и основание.
При решении логарифма lg также важно знать некоторые свойства логарифмических выражений, такие как: логарифм от единицы по любому основанию равен нулю (lg(1) = 0), а логарифм от нуля по любому основанию является неопределенным (lg(0) = -∞).
Решение логарифма лежит в основе множества математических и программных задач. Понимание основных методов решения логарифма позволяет более эффективно работать с математическими моделями, алгоритмами и программированием в целом.
Десятичный логарифм
Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика - Умскул
Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.
ЗАЧЕМ НУЖНЫ ЭТИ ... логарифмы! Математика на QWERTY
Логарифмы в ЕГЭ⚡️что получилось?!
Логарифмы с нуля. Определение. Свойства. Примеры. Решение логарифмов. Логарифмические свойства.