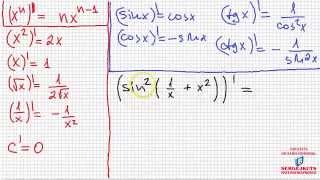КАК НАЙТИ ГРАДИЕНТ ФУНКЦИИ

Градиент функции является важным понятием в математике и оптимизации. Он представляет собой вектор, указывающий направление наибольшего возрастания функции в каждой точке.

Для нахождения градиента функции необходимо вычислить частные производные функции по каждой из ее переменных. Для функции, зависящей от одной переменной, градиент представляет собой обычную производную этой функции.

Для функции, зависящей от нескольких переменных, градиент вычисляется путем нахождения частных производных функции по каждой переменной и объединения их в вектор. Например, если у нас есть функция f(x, y), то градиент этой функции будет представлен вектором (df/dx, df/dy).

Градиент функции позволяет определить направление наибольшего возрастания функции в каждой точке. В точке, где градиент равен нулю, функция достигает своего локального максимума или минимума. Таким образом, градиент функции играет важную роль в оптимизации, поиске минимума или максимума функции.

Для вычисления градиента функции в программировании и алгоритмах существуют различные методы и алгоритмы, такие как градиентный спуск. Градиентный спуск является итеративным методом оптимизации, который использует градиент функции для поиска минимума функции. Этот метод широко применяется в машинном обучении и нейронных сетях.

Градиент в точке.

Градиент

GACHA LIFE 2 ОБЗОР - 2 часть, туториал

Градиент

Лекция. Градиентная оптимизация

«Можно блокировать женское образование»: Ася Казанцева — о работе мозга, демографии и чувстве вины