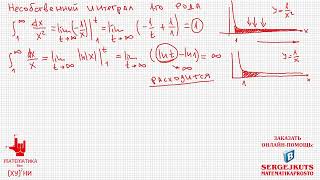КАК ОПРЕДЕЛИТЬ ЧАСТНОЕ ЗНАЧЕНИЕ ФУНКЦИИ
Частное значение функции определяется путем деления значения функции на аргумент. Для нахождения частного значения функции сначала необходимо вычислить значение функции для заданного аргумента, а затем разделить его на этот аргумент. В общем случае, если у нас есть функция f(x), чтобы найти частное значение функции для аргумента x, необходимо выполнить следующую операцию: f(x) / x. Это позволяет определить, как меняется значение функции при изменении аргумента.
Для примера, рассмотрим функцию f(x) = 2x + 3. Чтобы найти частное значение этой функции для аргумента x = 5, мы подставляем значение x в функцию и выполняем вычисления: f(5) = 2 * 5 + 3 = 13. Затем, для определения частного значения функции, мы делим полученный результат на аргумент: 13 / 5 = 2.6. Таким образом, частным значением функции f(x) для аргумента x = 5 является 2.6.
Если функция является сложной или состоит из нескольких функциональных частей, процесс нахождения частного значения может быть более сложным. В таких случаях необходимо последовательно применять алгоритм деления значения функции на аргумент. Важно учитывать особенности функции и правила работы с ней при определении частного значения.
Наибольшее и наименьшее значение функции. 10 класс.
ПРОИЗВОДНАЯ функции. Объяснение математического смысла.
Частные производные функции многих переменных
Свойства функции. Четность и нечетность функции. 10 класс.
Вы квасили капусту неправильно! Эти рекомендации превратят ее в лекарство
Математика без Ху%!ни. Частные производные функции нескольких переменных. Градиент.
Как исследовать функции? - Математика