КАК НАЙТИ ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ТРИГОНОМЕТРИЧЕСКОЙ ФУНКЦИИ
Промежутки возрастания и убывания тригонометрической функции определяются по её производной. Для этого необходимо найти производную функции и проанализировать её поведение.
Например, рассмотрим функцию синуса (sin(x)). Её производная равна косинусу (cos(x)). Промежутки возрастания синуса соответствуют точкам, где косинус положителен, а промежутки убывания - точкам, где косинус отрицателен. Также следует учитывать, что синус периодичен с периодом 2π.
Для определения промежутков возрастания и убывания тригонометрической функции необходимо найти точки, в которых производная функции обращается в ноль. Это могут быть максимумы или минимумы функции, а также точки перегиба. Для точного анализа поведения функции рекомендуется построить график исследуемой функции и её производной.
Важно отметить, что эти методы применимы не только к функции синуса, но и к другим тригонометрическим функциям, таким как косинус, тангенс, котангенс, секанс и косеканс.
Промежутки возрастания и убывания функции. Практическая часть. 10 класс.
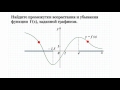
13A.1 Найдите промежутки возрастания и убывния функции f(x), заданной графиком
Промежутки возрастания и убывания функции. 10 класс.
Промежутки возрастания и убывания функции. Практическая часть. 10 класс.
ВИДЕО-УРОКИ. ПОДГОТОВКА К ЕГЭ ПРОФИЛЬ. ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ
Свойства функции. Четность и нечетность. Практическая часть. 10 класс.
Свойства функции. Промежутки возрастания и убывания функции. 10 класс.
График функции y=sinx и ее свойства. 10 класс.
Тригонометрические функции, y=tgx и y=ctgx, их свойства и графики. 10 класс.
Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.