КОГДА У ФУНКЦИИ НЕТ ПРЕДЕЛА
Когда функция не имеет предела, это означает, что не существует конечного значения, к которому она стремится по определённому предельному значению аргумента. Такое поведение функции может возникать по разным причинам.
Одна из основных причин - разрыв функции. Разрывы могут быть точечными или различными по свойствам. Если функция имеет точечный разрыв, то значит, что существует одна или несколько точек области определения, в которых функция не определена или значение функции разрывается. Если функция имеет разрыв, обусловленный свойствами функции, то это означает, что функция не может принять определённое значение на всей области определения.
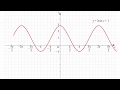
Другой причиной отсутствия предела может быть бесконечный рост или спад функции. Если функция стремится к бесконечности по значению, то говорят о бесконечном пределе. Например, функция f(x) = 1/x имеет бесконечный предел при x стремящемся к 0, поскольку значение функции увеличивается или уменьшается безгранично, приближаясь к бесконечности. Аналогично, функция может иметь отрицательный бесконечный предел, когда значения функции стремятся к минус бесконечности.
Также, функция может иметь пределы только с одной стороны. Например, функция f(x) = 1/x имеет предел +∞, если x стремится к 0 справа, но не имеет предела, если x стремится к 0 слева. Это означает, что функция может приближаться к определённому значению только с определённой стороны аргумента.
Следует отметить, что отсутствие предела не всегда означает, что функция не имеет значимости или не может использоваться. Некоторые функции могут быть полезными и иметь чёткое поведение на определённых интервалах области определения, даже если у них нет предела.
ПРЕДЕЛ ФУНКЦИИ. Артур Шарифов
Матан. Пределы для успешной сдачи зачёта - TutorOnline Математика
Что такое ПРЕДЕЛЫ. Математика на QWERTY
Предел функции на бесконечности. 10 класс.
Математика без Ху%!ни. Непрерывность функции, точки разрыва.
21. Доказательство предела функции по определению, примеры 1,2.
✓ Предел функции. Определение предела функции \