СКОЛЬКО ИНТЕРВАЛОВ ВОЗРАСТАНИЯ ИМЕЕТ ФУНКЦИЯ F Х Х3 3Х

Функция f(x) = x³ - 3x - является кубической функцией. Для определения интервалов возрастания функции необходимо найти ее производную и исследовать знаки производной на различных интервалах.

Производная функции f(x) равна f'(x) = 3x² - 3. Для определения знаков производной необходимо решить неравенство 3x² - 3 > 0.

Решая это неравенство, получаем x² > 1, что эквивалентно x < -1 или x > 1.

Исследуя знаки производной на интервалах (-∞, -1), (-1, 1) и (1, +∞), мы можем сделать следующие выводы о функции:

1. На интервале (-∞, -1) производная f'(x) < 0, следовательно, функция f(x) убывает на этом интервале;
2. На интервале (-1, 1) производная f'(x) > 0, следовательно, функция f(x) возрастает на этом интервале;
3. На интервале (1, +∞) производная f'(x) < 0, следовательно, функция f(x) убывает на этом интервале.

Таким образом, функция f(x) имеет один интервал возрастания (-1, 1).

Математический анализ, 34 урок, Экстремум функции двух переменных

АЛГЕБРА С НУЛЯ — Точки Экстремума Функции

Функция. Область определения функции. Практическая часть. 10 класс.

10 класс, 44 урок, Применение производной для исследования функций на монотонность и экстремумы

Свойства функции. Четность и нечетность функции. 10 класс.

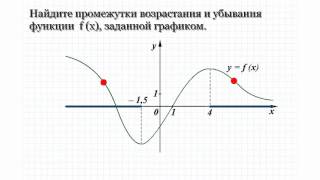
13A.1 Найдите промежутки возрастания и убывния функции f(x), заданной графиком