Как Решать Показательные Неравенства С Логарифмами

Показательные неравенства, содержащие логарифмы, могут быть решены с помощью различных методов. Важно понимать, что при работе с логарифмами мы можем применять различные свойства и правила для упрощения и анализа неравенств.

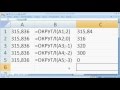
Одним из основных методов решения показательных неравенств с логарифмами является приведение неравенства к эквивалентной форме без логарифмов. Для этого мы используем свойства логарифмов и решаем получившееся уравнение.

Примерно такой метод решения:

1. Изначально имеем показательное неравенство с логарифмами.

2. Путем применения свойств логарифмов преобразуем исходное неравенство таким образом, чтобы мы получили эквивалентное уравнение без логарифмов. При этом не забываем учесть допустимые области определения логарифмов и их основания.

3. Решаем полученное уравнение без логарифмов. Для этого мы можем применять различные методы, включая приведение подобных слагаемых, факторизацию или применение формул решения алгебраических уравнений.

4. Получаем множество решений исходного показательного неравенства с логарифмами в виде интервалов или числовых неравенств.

Имейте в виду, что решение показательных неравенств с логарифмами может быть сложным и требовать дополнительного анализа и применения нестандартных методов в зависимости от конкретной задачи. Поэтому важно понимать основы работы с логарифмами и иметь хорошее математическое образование для успешного решения подобных неравенств.