Как Найти Математическое Ожидание По Функции Распределения

Математическое ожидание является одним из основных понятий в теории вероятностей и статистике. Оно позволяет оценить среднее значение случайной величины и представляет собой взвешенную сумму всех возможных значений с учетом их вероятностей.

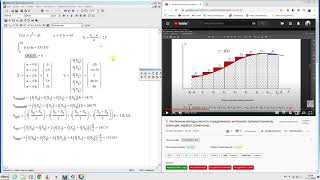
Для нахождения математического ожидания по функции распределения необходимо следовать определенному алгоритму. Первым шагом является определение функции распределения случайной величины. Функция распределения представляет собой функцию, которая описывает вероятность получения данного значения случайной величины или меньшего значения.

После определения функции распределения необходимо найти производную этой функции. Полученная производная называется плотностью вероятности и обозначается f(x). Плотность вероятности представляет собой функцию, которая показывает вероятность получения определенного значения случайной величины.

Далее необходимо умножить значение плотности вероятности на значение случайной величины (x) и проинтегрировать полученное выражение по всем возможным значениям случайной величины. Интеграл от произведения плотности вероятности и значения случайной величины по всем возможным значениям представляет собой математическое ожидание.

Таким образом, чтобы найти математическое ожидание по функции распределения, необходимо определить функцию распределения, найти плотность вероятности, произвести умножение плотности на значение случайной величины и проинтегрировать полученное выражение по всем возможным значениям случайной величины.