Как По Графику Производной Найти Наименьшее Значение Функции

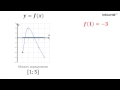
Для определения наименьшего значения функции по графику производной, необходимо проанализировать точки, где производная равна нулю или не определена.

Когда производная функции равна нулю, это может указывать на экстремумы функции - минимумы или максимумы. Такие точки называются критическими точками. Если производная меняет знак с отрицательного на положительный в критической точке, это указывает на наименьшее значение функции.

Чтобы найти критические точки функции, необходимо решить уравнение производной равной нулю. Затем, анализируя изменение производной, определить, является ли каждая критическая точка минимумом или максимумом.

Если производная функции не определена в какой-либо точке, это может указывать на разрыв или вертикальную асимптоту. В таких случаях наименьшее значение функции может быть найдено, проверяя значения функции вблизи разрыва или асимптоты.

Таким образом, анализируя график производной функции и рассматривая критические точки и точки разрыва, можно найти наименьшее значение функции.