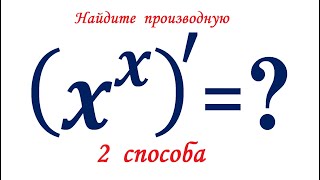КАК НАЙТИ ПРОИЗВОДНУЮ ФУНКЦИИ В ТОЧКЕ
Производная функции в точке является одной из основных понятий математического анализа. Она позволяет определить скорость изменения функции в данной точке, а также найти уравнение касательной к графику функции.
Для нахождения производной функции в точке используется понятие предела. Если функция задана аналитически, то можно найти ее производную с помощью правил дифференцирования. Например, для вычисления производной степенной функции, нужно умножить показатель степени на коэффициент перед x и уменьшить показатель степени на единицу.
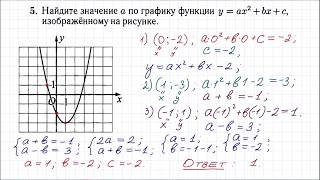
Если функция задана графически или в виде таблицы значений, то можно оценить производную, используя пределы и формулу приближенного вычисления производной. Для этого выбирается точка достаточно близко к исследуемой и находится разница между значениями функции в двух соседних точках. Затем разница делится на разницу входных параметров. Чем меньше будет разность значений и входных параметров, тем ближе будет приближенное значение производной к истинному.
Наличие производной в точке позволяет определить, является ли функция непрерывной в данной точке. Если производная существует в данной точке, она будет определена и в некоторой окрестности этой точки.
Важно помнить, что производная функции в точке не всегда существует. Некоторые функции могут иметь разрывы или быть неопределенными в определенных точках. В таких случаях производную нельзя найти или она не имеет смысла.
Нахождение производной функции в точке имеет множество приложений в различных областях, включая физику, экономику, инженерию и другие науки. Оно позволяет оптимизировать процессы и решать различные задачи, связанные с изменением величин.
Математика Без Ху%!ни. Производная сложной функции.
АЛГЕБРА С НУЛЯ — Что такое Производная?
Найти значение производной в точке.
Производная в точке. Алгебра 10 и 11 класс.
Как тут все устроено. Почему тупик это норм + тест (какой твой уровень) Спиральная динамика
Производная функции. 10 класс.
Математика без Ху%!ни. Частные производные функции нескольких переменных. Градиент.