КАК НАЙТИ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ СТЕПЕННОЙ ФУНКЦИИ
Степенные функции в математике являются важным классом функций, которые имеют вид f(x) = ax^n, где a и n - постоянные числа, а x - переменная. Как найти наибольшее и наименьшее значение такой степенной функции?
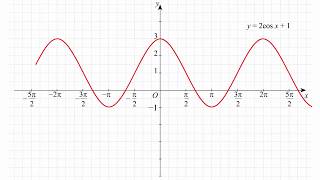
Для нахождения наибольшего и наименьшего значения степенной функции необходимо использовать знание об особенностях ее графика. При анализе графика степенной функции f(x) = ax^n возможно выделить несколько случаев.
1. Когда показатель степени n - четное число, то график функции имеет форму параболы, открывающейся вверх при положительном a и вниз при отрицательном a. Наибольшее значение функции будет находиться в вершине параболы, а наименьшее значение - на одном из концов графика. Для нахождения вершины параболы можно использовать формулу x = -b/(2a), где b - коэффициент при x в формуле функции.
2. Если показатель степени n - нечетное число, то график функции будет либо всегда возрастающим, либо всегда убывающим, в зависимости от знака коэффициента a. В этом случае, наименьшее значение функции можно найти при x, стремящемся к минус бесконечности, а наибольшее - при x, стремящемся к плюс бесконечности.
Таким образом, нахождение наибольшего и наименьшего значения степенной функции связано с исследованием ее графика и определением его особенностей в зависимости от переменных a и n. Этот анализ позволяет определить точки, в которых функция достигает наибольших и наименьших значений.
11 класс, 9 урок, Степенные функции, их свойства и графики
Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезке
Наибольшее и наименьшее значение функции. 10 класс.
Алгебра 10 класс. 13 сентября. Наименьшее и наибольшее значение функции #2
Степенная функция и ее свойства. 11 класс.
Алгебра 10 класс. 12 сентября. Наименьшее и наибольшее значение функции