КАК ИЗВЕСТНО ЧТОБЫ ПОСТРОИТЬ ГРАФИК КАКОЙ ЛИБО МАТЕМАТИЧЕСКОЙ ФУНКЦИИ НЕОБХОДИМО ОПРЕДЕЛИТЬ ЕЕ

Каждая математическая функция может быть представлена графически, что помогает наглядно представить ее поведение и свойства. Для построения графика любой математической функции необходимо определить ее свойства, такие как область определения и значения функции.

Область определения функции указывает на все значения переменных, при которых функция имеет смысл. Затем необходимо вычислить значения функции для различных значений независимой переменной и составить таблицу пар значений (x, f(x)).

Следующим шагом является построение координатной плоскости, где ось X представляет значения независимой переменной (x), а ось Y - значения функции (f(x)). Затем все пары значений из таблицы отмечаются на графике. После этого можно связать отмеченные точки, получив график функции.

График помогает визуализировать различные свойства функции, такие как возрастание, убывание, экстремумы, пересечения с осями координат и асимптоты. Он также позволяет проводить дальнейшие исследования и анализировать поведение функции в различных областях.

Математический анализ, 16 урок, Исследование функции и построение графика

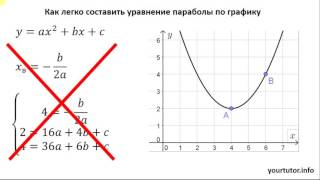
Где ПАРАБОЛА пригодится в жизни?

Совмещение графиков в MS Excel (построение комбинированного графика)

Квадратичная функция за 5 минут

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график Парабола

Как запомнить графики функций

Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.

Матан за час. Шпаргалка для первокурсника. Высшая математика