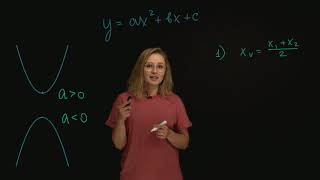Как Найти Локальные Экстремумы Функции

Как найти локальные экстремумы функции?

Поиск локальных экстремумов функции является важной задачей в математике и оптимизации. Локальные экстремумы представляют собой точки, где функция достигает максимума или минимума в определенной окрестности.

Существует несколько методов для нахождения локальных экстремумов. Один из них – использование производных функции. Если производная равна нулю в точке, то это может быть точка экстремума. Также можно анализировать знак производной: если производная меняется с положительного на отрицательное значение, то это может быть точкой максимума, и наоборот.

Другой метод – использование второй производной функции. Если вторая производная положительна в точке, то это может быть точка минимума, и наоборот.

Также существуют и другие методы, такие как метод половинного деления (или метод бисекции), метод золотого сечения, метод Ньютона и другие численные методы, которые позволяют находить локальные экстремумы функции с заданной точностью.

Поиск локальных экстремумов функции является важным инструментом в различных областях, таких как оптимизация, математическое моделирование, экономика и другие. Правильный выбор метода и алгоритма может значительно ускорить решение задачи и улучшить результаты.