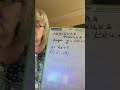КАК РЕШАТЬ КВАДРАТНЫЕ УРАВНЕНИЯ С ЛОГАРИФМАМИ
Квадратные уравнения с логарифмами являются особым видом уравнений, где переменная появляется не только в квадратичном члене, но и в логарифмической функции. Для решения таких уравнений, требуется применить специальные методы и техники.
Один из подходов к решению квадратных уравнений с логарифмами - это приведение уравнения к экспоненциальной форме. Для этого необходимо использовать свойства логарифмов и экспоненты для перевода логарифмических функций в экспоненциальную форму.
Пример решения квадратного уравнения с логарифмами:
Дано уравнение: log(x^2 + 3x - 2) = 2
Шаг 1: Преобразование логарифма в экспоненциальную форму:
x^2 + 3x - 2 = 10^2
Шаг 2: Приведение квадратного уравнения в стандартную форму:
x^2 + 3x - 2 - 100 = 0
Шаг 3: Решение уравнения с помощью факторизации, полного квадрата или квадратного корня:
Применяя соответствующий метод, находим значения x, которые удовлетворяют уравнению.
Шаг 4: Проверка найденных корней:
Подставляем найденные значения x обратно в исходное уравнение для проверки их правильности.
Важно отметить, что решение квадратных уравнений с логарифмами может иметь несколько корней или быть пустым, в зависимости от конкретного уравнения.
Таким образом, решение квадратных уравнений с логарифмами требует использования специальных методов и понимания свойств логарифмов и экспоненты.
✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов - Борис Трушин
Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.
Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика - Умскул
Лукашенко ближе к ордеру
Редкое уравнение ➜ Логарифмы с разными основаниями
Пятиминутки № 042. Двойное фианкетто за черных. Гиппопотам в действии
Проще простого! Как решить Логарифмическое Уравнение?