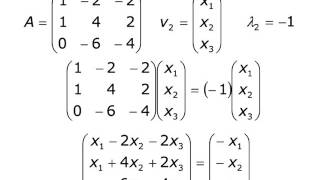КАК РЕШАТЬ УРАВНЕНИЯ С ЛОГАРИФМАМИ

Уравнения с логарифмами являются одним из важных разделов в математике. Решение таких уравнений требует применения специальных методов и правил.

Одним из основных способов решения уравнений с логарифмами является использование свойств логарифмов. При решении таких уравнений мы стараемся привести их к виду, где можно применить эти свойства.

Для начала, мы можем использовать основное свойство логарифма, которое гласит, что логарифм от произведения двух чисел равен сумме логарифмов этих чисел:

log_b(xy) = log_b(x) + log_b(y)

Также, мы можем применить другое свойство логарифма, которое гласит, что логарифм от деления двух чисел равен разности логарифмов этих чисел:

log_b(x/y) = log_b(x) - log_b(y)

Используя эти свойства, мы можем приступить к решению уравнений с логарифмами. Сначала мы ищем возможность привести уравнение к виду, где все логарифмы находятся по одну сторону от равенства.

Затем, мы применяем свойства логарифмов, чтобы избавиться от логарифмов и свести уравнение к обычному уравнению, которое можно решить методами алгебры.

Важно помнить, что при решении уравнений с логарифмами необходимо проверять полученные решения, так как некоторые значения могут быть недопустимыми для исходного уравнения.

В заключение, решение уравнений с логарифмами - это процесс, требующий применения свойств логарифмов и алгебраических методов. При правильном применении этих методов можно получить корректные решения для уравнений данного типа.

ЕГЭ база #7 / Логарифмические уравнения / Свойства, определение логарифма / решу егэ

Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.

Круговорот воды в природе ➜ Решение логарифмических уравнений из ЕГЭ #Shorts

Сложные уравнения. Как решить сложное уравнение?

Logarifm haqida dastlabki tushunchalar - Logarifmlar - Algebra 2

✓ Как решать логарифмические уравнения и неравенства, не помня свойства логарифмов - Борис Трушин