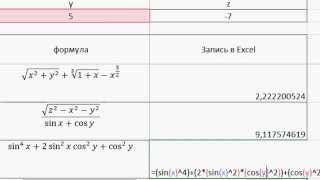
Как Найти Значение Функции От Матрицы

Матрицы являются важным инструментом в математике и представляют собой упорядоченную таблицу чисел, разделенных на строки и столбцы. Зачастую в математических и программных задачах требуется найти значение функции от матрицы. Для этого необходимо применить функцию к каждому элементу матрицы и получить новую матрицу с результатами.

Процесс нахождения значения функции от матрицы может варьироваться в зависимости от самой функции. Некоторые функции могут выполняться поэлементно, то есть применяться к каждому элементу матрицы независимо. Другие функции могут иметь более сложное определение и требовать определенных операций или алгоритмов для вычисления значения.

Например, если требуется найти сумму элементов матрицы, можно пройти по каждому элементу матрицы и добавить его значение к накопленной сумме. Аналогично, для нахождения произведения элементов матрицы можно последовательно умножать каждый элемент на предыдущий результат.

Для нахождения значения более сложных функций от матрицы могут использоваться различные алгоритмы. Например, для нахождения определителя матрицы применяются специальные методы, такие как метод Гаусса или разложение ЛУ.

В программировании часто используются специализированные библиотеки и функции, которые облегчают работу с матрицами и вычислениями. Например, в языке Python есть библиотека NumPy, которая предоставляет множество функций для работы с матрицами и выполнения различных операций над ними.

В конечном итоге, нахождение значения функции от матрицы зависит от самой функции и требуемых операций. Необходимо определить, как функция должна быть применена к элементам матрицы, и выбрать подходящий метод или алгоритм для получения результата.