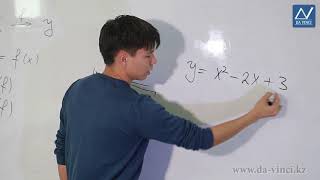КАКОЙ УГОЛ ОБРАЗУЕТ КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ Y X2 4X 5
Когда мы говорим о графике функции y = x^2 + 4x + 5, у нас возникают вопросы о взаимодействии касательной и функции. Какой же угол образует касательная с графиком данной функции?
Для определения угла, образуемого касательной с графиком функции, нам необходимо знать точку касания. К сожалению, в данном случае точка касания не указана. Поэтому мы не можем определить точный угол, образуемый касательной с графиком функции y = x^2 + 4x + 5.
Тем не менее, мы можем обучиться некоторым принципам, чтобы узнать, как работает касательная. Касательная к графику функции в определенной точке является прямой, которая проходит через эту точку и имеет тот же наклон, что и график в этой точке. Угол между этой касательной и осью абсцисс называется углом наклона или углом касательной.
Чтобы вычислить угол касательной в какой-либо точке, нам нужно использовать производную функции в этой точке. Производная функции y = x^2 + 4x + 5 равна 2x + 4. Однако нам не хватает конкретной точки для вычисления угла.
Поэтому, чтобы ответить на вопрос о том, какой угол образует касательная к графику функции y = x^2 + 4x + 5, необходимо знать точку касания касательной с графиком. Без этой информации мы не можем дать точного ответа.
Построение графика функции y=-f(x)- и y=f(-x-)
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
Как написать уравнения касательной и нормали - Математика
Задание 5 ОГЭ по математике
Касательная к графику функции в точке. 10 класс.
10 класс, 43 урок, Уравнение касательной к графику функции
Задание 7 ЕГЭ по математике
Математика без Ху%!ни. Уравнение касательной.
График функции y=x² (y=аx).