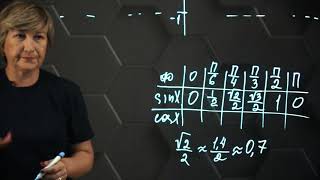Как Называются Графики Тригонометрических Функций

Графики тригонометрических функций представляют собой изображения зависимостей значений этих функций от аргумента. Известно, что тригонометрические функции включают синус, косинус, тангенс, котангенс, секанс и косеканс. Каждая из этих функций имеет свой график и характерные особенности.

График синуса (y = sin(x)) представляет собой периодическую функцию с амплитудой, которая колеблется в диапазоне от -1 до 1. Он обладает симметрией относительно начала координат и имеет особенность точек перегиба в точках (π/2, 1) и (3π/2, -1).

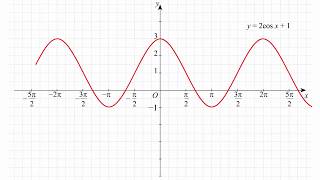
График косинуса (y = cos(x)) также является периодической функцией с амплитудой от -1 до 1. Он имеет симметрию относительно оси ординат и основные точки перегиба в точках (0, 1) и (π, -1).

График тангенса (y = tan(x)) представляет собой периодическую функцию с вертикальными асимптотами в точках (π/2 + πk, k ∈ ℤ). Он имеет особенность точки разрушения графика в точках (π/2 + πk, ±∞).

График котангенса (y = cot(x)) также является периодической функцией и имеет горизонтальные асимптоты в точках (πk, k ∈ ℤ). У него есть точка разрушения графика в точках (πk, ±∞).

График секанса (y = sec(x)) представляет собой периодическую функцию с вертикальными асимптотами в точках ((2k + 1)π/2, k ∈ ℤ). Он имеет характерные точки разрушения графика в точках ((2k + 1)π/2, ±∞).

График косеканса (y = csc(x)) также является периодической функцией и имеет горизонтальные асимптоты в точках (kπ, k ∈ ℤ). У него есть точка разрушения графика в точках (kπ, ±∞).