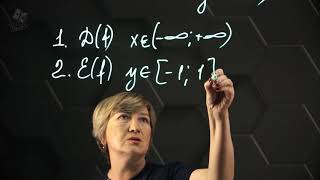КОГДА ФУНКЦИЯ ОБРАТИМА

Функция обратима, когда она имеет обратную функцию, то есть, существует такая функция, которая отображает обратно каждое значение, полученное первоначальной функцией.

Когда функция является биекцией, то есть она однозначно отображает каждое значение из исходного множества в уникальное значение в целевом множестве, функция считается обратимой.

Для того чтобы функция была обратимой, необходимо, чтобы она была инъекцией (инекция) и сюръекцией (сюръекция). Инъекция означает, что разным элементам исходного множества соответствуют разные элементы в целевом множестве. Сюръекция означает, что каждый элемент целевого множества имеет прототип в исходном множестве.

Если функция не является инъекцией, то есть разным значениям из исходного множества соответствуют одинаковые значения в целевом множестве, она не будет обратимой. Точно так же, если функция не является сюръекцией, то есть есть элементы в целевом множестве, которым не соответствует ни один элемент исходного множества, она также не будет обратимой.

Помимо этого, чтобы функция была обратима, важной характеристикой является определенность значения функции. Если для одного и того же аргумента значение функции может быть каким-то из нескольких возможных значений, то функция не будет обратимой.

Таким образом, функция обратима, когда она является биекцией и имеет однозначное определение значения для каждого элемента исходного множества.

Математика, 10-й класс, Обратимые функции. Обратная функция

10 класс алгебра обратная функция

Обратимость и необратимость химических реакций. Химическое равновесие. 1 часть. 9 класс.

10 класс, 10 урок, Обратная функция

Уравнение, которое меняет взгляд на мир [Veritasium]

Взаимно обратные функции. Теория. Видеоурок 6. Алгебра 10 класс

ВЗАИМНО ОБРАТНЫЕ ФУНКЦИИ

Обратная функция. Введение