КАК РЕШАТЬ НЕРАВЕНСТВА С СИНУСОМ ТРИГОНОМЕТРИЧЕСКИЕ
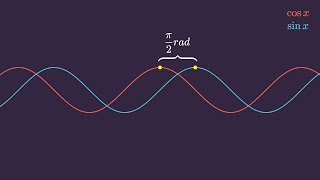
Неравенства с синусом являются одним из видов тригонометрических неравенств. Для их решения необходимо использовать свойства синуса и обратных тригонометрических функций.
Для начала рассмотрим случай, когда неравенство представлено в виде sin(x) > k, где k - некоторое число от -1 до 1.
1. Находим наименьшее и наибольшее значение, которое может принимать sin(x) в данном интервале. Для этого используем свойства синуса и ограничения на x.
2. Затем с помощью обратных тригонометрических функций находим все x, для которых sin(x) > k. Например, если k = 0, то решением будет x ∈ (0, π) ∪ (2π, 3π), так как sin(x) > 0 для значений x из этих интервалов.
3. Искомое множество решений представляет собой объединение всех найденных интервалов с x.
Аналогично решаются неравенства типа sin(x) < k, sin(x) ≥ k и sin(x) ≤ k.
Если неравенство задано в виде sin(x) < sin(a), где a - некоторый угол, то применяем следующие шаги:
1. Приводим оба выражения в одинаковую форму, используя тригонометрические тождества и свойства синуса.
2. Приравниваем аргументы синусов и решаем полученное уравнение.
3. Исследуем полученные решения и определяем множество x, для которых sin(x) < sin(a).
Таким образом, решение тригонометрических неравенств с синусом сводится к использованию свойств синуса и обратных тригонометрических функций, а также применению тригонометрических тождеств и анализу интервалов, на которых меняется значение sin(x).
10 класс, 22 урок, Простейшие тригонометрические уравнения неравенства
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по Математике
Как решать тригонометрические неравенства?
Решение тригонометрических неравенств. 10 класс.
Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.
Невозможная сингапурская задача
Решение тригонометрических уравнений. Подготовка к ЕГЭ - Математика TutorOnline