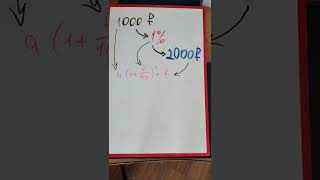Как Разложить Интеграл

Интеграл - это математический объект, связанный с понятием площади или нахождения некоторого значения. Разложение интеграла является важным методом, позволяющим упростить его вычисление или представить в другой форме.

Существует несколько различных методов и приемов разложения интеграла, в зависимости от задачи и типа интеграла. Один из наиболее популярных методов - разложение на простые дроби.

Разложение интеграла на простые дроби основывается на представлении рациональной функции в виде суммы простых дробей. Этот метод позволяет вычислить интеграл от рациональной функции, разбив его на сумму более простых интегралов. В результате получается более удобная форма интеграла для последующего вычисления.

Для разложения интеграла на простые дроби необходимо выполнить следующие шаги:

Разложить рациональную функцию на частные дроби. Для этого проводятся определенные алгебраические действия с числителем и знаменателем функции.
Разложить каждую частную дробь на сумму простых дробей. В этом шаге требуется понимание того, как выразить частную дробь в виде суммы дробей с простыми знаменателями.
Найти неизвестные коэффициенты разложения, решая систему уравнений, составленную на основе изначальной рациональной функции.
Проверить правильность разложения, произведя обратную операцию и сложив простые дроби обратно в рациональную функцию. Результат должен совпадать с изначальной функцией.

Разложение интеграла на простые дроби является комплексным процессом, требующим математической подготовки и понимания алгебраических операций. Он широко применяется в вычислительной математике, инженерии и физике для решения различных задач, связанных с интегрированием.