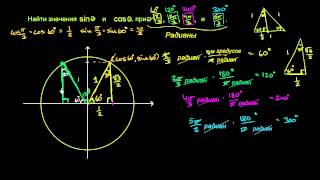
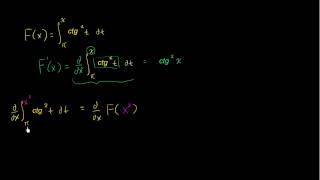КАК РЕШАТЬ ИНТЕГРАЛЫ С СИНУСОМ И КОСИНУСОМ

Интегрирование функций, содержащих синусы и косинусы, является одним из ключевых заданий в математике и анализе. Решение таких интегралов требует применения определенных методов, которые позволяют найти аналитические выражения для этих функций.

Для решения интегралов с синусами и косинусами следует использовать технику интегрирования по частям. Этот метод основан на интегрировании произведения двух функций. Первая функция выбирается так, чтобы ее производная была интегрируема, в данном случае это синус или косинус. Вторая функция выбирается так, чтобы ее интеграл был легко вычисляемым.

Процесс решения интегралов с синусами и косинусами включает следующие шаги:

1. Выберите первую функцию и вторую функцию для интегрирования по частям (синус или косинус для первой функции и остаток для второй функции).
2. Примените формулу для интегрирования по частям: ∫(u·v)dx = u·∫vdx - ∫(u'·∫vdx)dx, где u - первая функция, v - вторая функция, u' - производная первой функции.
3. Получившийся интеграл разделите на два слагаемых и продолжайте применять интегрирование по частям, пока не достигнете интеграла, который можно легко вычислить.
4. Вычислите значения полученных интегралов и приведите ответ к окончательному виду.

Приведенный выше метод является одним из основных подходов к решению интегралов с синусами и косинусами. Однако, для некоторых интегралов могут потребоваться дополнительные методы, такие как замена переменной, тригонометрические тождества, или применение специальных таблиц интегралов.

Интегралы с синусами и косинусами широко используются в различных областях математики, физики, инженерии, и других науках. Они играют важную роль в решении дифференциальных уравнений, моделировании колебательных систем, определении площади под кривыми, и многих других приложениях.

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия - Математика

7.1 Интегралы от тригонометрических функций Примеры

Математика- Преобразование тригонометрических выражений. Формулы и задачи

Интеграл (cos x)^n. Общая формула

Главная ТАЙНА соционики — посмотри это перед тестом на тип личности

Зачем нужны синусы и косинусы?

7.5 Интегралы от тригонометрических функций / интеграл от синуса и косинуса в степени

Математика без Ху%!ни. Интегралы, часть 3. Замена переменной.