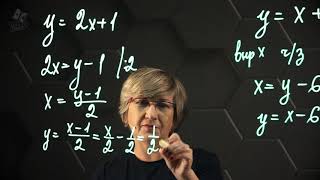Как Привести Интеграл К Табличному Виду

Интегралы - это важный элемент математического анализа, и их вычисление может быть сложной задачей. Однако существуют различные методы, которые позволяют привести интегралы к табличному виду, делая их вычисление более простым и удобным.

Один из таких методов - метод замены переменной. При использовании этого метода, мы заменяем исходную переменную интеграла на новую переменную, которая позволяет упростить выражение и привести его к табличному виду. Замена переменной может быть осуществлена с помощью различных подстановок, формул или тригонометрических тождеств, в зависимости от конкретного интеграла.

Еще одним методом является метод интегрирования по частям. Этот метод основывается на формуле интегрирования произведения двух функций и позволяет свести интеграл к табличному виду. При применении этого метода, мы выбираем одну функцию в качестве первой производной, а другую функцию в качестве второй, и применяем соответствующую формулу.

Однако, чтобы привести интеграл к табличному виду, необходимо уметь идентифицировать соответствующий метод и применить его с использованием соответствующих формул и преобразований. Для этого важно знать основные приемы и придерживаться определенных правил интегрирования.

Таким образом, с использованием различных методов, таких как метод замены переменной и метод интегрирования по частям, интегралы могут быть приведены к табличному виду, что позволяет упростить вычисление их значений. Овладев этими методами и правилами, можно успешно решать задачи, связанные с интегрированием и анализом функций.