КАК НАЙТИ ПЛОЩАДЬ КРУГА ЧЕРЕЗ ИНТЕГРАЛ
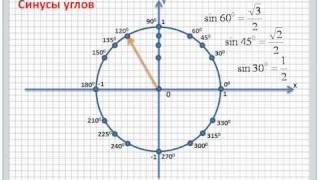
Для вычисления площади круга с помощью интеграла необходимо использовать представление круга в полярных координатах. В полярной системе координат радиус круга задается функцией r(θ), где r - радиус круга, а θ - угол, измеряемый от положительного направления оси OX.
Для определения границ интегрирования используется угловой диапазон от 0 до 2π, который соответствует полному обороту вокруг центра круга.
Площадь элементарной полосы круга, ограниченной линиями с углами θ и θ + dθ, определяется как dA = (1/2)r²dθ.
Интегрируя эти элементарные полосы от 0 до 2π, мы получим полную площадь круга:
S = ∫[0,2π](1/2)r²dθ.
Используя формулу для площади круга, S = πr², мы можем записать интеграл следующим образом:
πr² = ∫[0,2π](1/2)r²dθ.
Интегрируя это выражение, получаем окончательную формулу для вычисления площади круга через интеграл:
S = ∫[0,2π](1/2)r²dθ = πr².
Площадь фигуры через двойной интеграл в полярных координатах
ТАКОГО НИКТО НЕ ОЖИДАЛ! ХИТРЫЙ ХОД РУБЛЯ! ЭТОТ ПРОГНОЗ ГУРИЕВА ПРИВЕЛ ВСЕХ В ЧУВСТВО!
Площадь круга через интеграл
Площадь круга. Математика 6 класс.
Как рассчитать сегменты .
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.
Лучший способ найти площадь круга