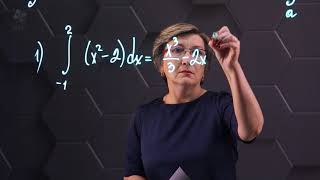КАК СОСТАВИТЬ УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ ПАРАЛЛЕЛЬНОЙ ПРЯМОЙ
Чтобы составить уравнение касательной к графику функции, параллельной прямой, необходимо знать две вещи: уравнение функции и угловой коэффициент прямой, к которой требуется построить касательную.
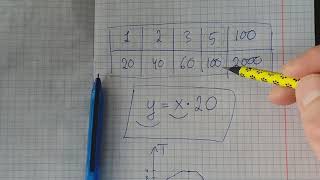
Пусть дана функция в виде уравнения y = f(x) и прямая в виде уравнения y = mx + c, где m - угловой коэффициент прямой, а c - её отрезок на оси ординат.
Чтобы найти точку касания касательной с графиком функции, решаем систему уравнений между функцией и прямой. Из системы можно найти координаты точки касания (x₀, y₀).
Затем используем найденные координаты (x₀, y₀) в уравнении прямой y = mx + c, чтобы найти значение углового коэффициента m₀ для касательной.
Итак, уравнение касательной к графику функции, параллельной прямой, имеет вид y = m₀x + (y₀ - m₀x₀), где m₀ - угловой коэффициент касательной, а (x₀, y₀) - координаты точки касания.
ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
10 класс, 43 урок, Уравнение касательной к графику функции
Реакция на результаты ЕГЭ 2022 по русскому языку
Самый короткий тест на интеллект Задача Массачусетского профессора
Математика без Ху%!ни. Уравнение касательной.