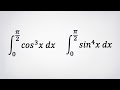Как Найти Особые Точки Функции

Особые точки функции - это значения аргумента, при которых функция имеет особенности, такие как разрывы, разрывные точки, асимптоты и максимальные/минимальные значения. Найти эти точки может быть важным шагом при анализе и изучении функций.

Для нахождения особых точек функции необходимо выполнить несколько шагов. Во-первых, нужно найти все точки, где функция становится неопределенной или разрывной. Это может произойти, например, когда знаменатель функции обращается в ноль или при появлении других условий разрыва.

Также следует исследовать поведение функции вблизи точек, где функция имеет разрывы или неопределенности. Для этого можно использовать левосторонний и правосторонний пределы, чтобы определить, является ли точка точкой разрыва или точкой асимптоты.

Если функция имеет асимптоты, то необходимо найти уравнения этих асимптот и определить их влияние на поведение функции в окрестности этих точек.

Для нахождения максимальных и минимальных значений функции следует производить дифференцирование и нахождение экстремумов. Учитывайте, что функция может иметь локальные и глобальные экстремумы, поэтому необходимо проверить значения функции на концах области определения и внутри этой области.

Найти особые точки функции может потребовать глубокого анализа функции и ее поведения. Важно учитывать особые случаи и особенности конкретной функции для того, чтобы определить все возможные особые точки.