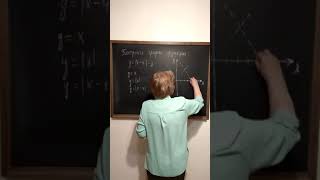КАК ДОКАЗАТЬ ИРРАЦИОНАЛЬНОСТЬ ЛОГАРИФМА

Доказательство иррациональности логарифма является одной из важных тем в математике. Иррациональность логарифма означает, что значение логарифма не может быть представлено в виде дроби и не является рациональным числом.

Существует несколько подходов к доказательству иррациональности логарифма. Один из них основан на рассмотрении разложений логарифма в бесконечную десятичную дробь и показывает, что эта дробь не повторяется и не может быть представлена в виде простой десятичной дроби.

Для доказательства иррациональности логарифма е используются техники из других областей математики, таких как теория чисел и теория вероятностей. Некоторые методы доказательства включают использование цепных дробей, тождества Эйлера и сходимость возможных разложений.

В итоге, доказательство иррациональности логарифма является трудной задачей, требующей глубоких знаний математики и применения различных методов. Однако, благодаря этому доказательству мы можем лучше понять и описать природу логарифмов и их математические свойства.

НЕРЕШЁННЫЕ ПРОБЛЕМЫ ШКОЛЬНОЙ МАТЕМАТИКИ, ВЕРСИЯ ОТ 29 МАРТА В ГОРОДЕ ПЕТРОЗАВОДСК!!!

Логарифмы с нуля за 30 минут. Логарифмы 10 класс ЕГЭ профиль математика - Умскул

✓ Как доказать иррациональность корней - Ботай со мной #120 - Борис Трушин

100 тренировочных задач #86 Доказать иррациональность логарифма

Иррациональность sqrt2

19. Число е как предел последовательности

Почти школьное доказательство иррациональности числа пи - Ботай со мной #073 - Борис Трушин -