КАК НАЙТИ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ЛИНЕЙНОЙ ФУНКЦИИ НА ЗАДАННОМ ПРОМЕЖУТКЕ 7 КЛАСС

При изучении линейных функций в 7 классе одной из важных задач является поиск наибольшего и наименьшего значения функции на заданном промежутке. Это позволяет определить экстремумы функции и понять ее поведение в данном интервале.

Для нахождения наибольшего и наименьшего значения линейной функции на заданном промежутке, необходимо использовать некоторые базовые знания и методы математического анализа.

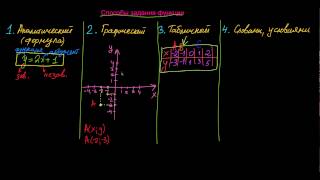
1. Сначала задайте линейную функцию в виде y = kx + b, где k - коэффициент наклона прямой, а b - свободный член.

2. Определите границы заданного промежутка и присвойте им значения. Обозначим эти значения как a и b, где a - начало интервала, а b - конец интервала.

3. Вычислите значения функции на границах промежутка. Подставьте значения a и b в уравнение функции и найдите соответствующие значения y_a и y_b.

4. Сравните полученные значения y_a и y_b. Если y_a > y_b, то наибольшим значением функции на заданном промежутке будет y_a, а наименьшим - y_b. В обратном случае наибольшим значением будет y_b, а наименьшим - y_a.

5. Для большей точности и уверенности в результатах, можно построить график функции и визуально определить экстремумы на заданном промежутке.

Таким образом, нахождение наибольшего и наименьшего значения линейной функции на заданном промежутке в 7 классе требует определения границ промежутка, подстановки значений границ в уравнение функции и сравнения полученных значений. Это поможет понять поведение функции и найти ее экстремумы в указанном интервале.

Наибольшее и наим. значения функции на отрезке

Алгебра 7 класс. 9 октября. Наименьшее и наибольшее значение функции на отрезке

как я учусь вязать носки ⭐️ книга \

Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline

Линейная функция и ее график. 7 класс.

Нахождение наибольшего и наименьшего значения функции по графику

Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезке