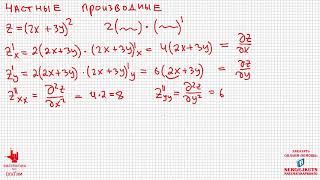ЧТО ТАКОЕ ГРАДИЕНТ ФУНКЦИИ
Градиент функции - это вектор, который указывает на направление наибольшего возрастания функции в конкретной точке. Он вычисляется путем взятия частных производных функции по каждой из ее переменных и объединении их в вектор. Градиент функции позволяет нам определить, куда двигаться от данной точки в пространстве переменных, чтобы достичь максимального или минимального значения функции.
Градиент функции имеет важное значение в оптимизации и машинном обучении. В методах оптимизации он используется для нахождения оптимальных значений параметров модели. Например, в алгоритме градиентного спуска, градиент функции используется для обновления параметров модели, чтобы минимизировать функцию потерь. Также градиент функции применяется в градиентных методах оптимизации, таких как стохастический градиентный спуск, адаптивный градиентный спуск и другие.
Важно отметить, что градиент функции может быть положительным или отрицательным в зависимости от направления наискорейшего возрастания функции. Модуль градиента указывает на скорость изменения функции в данной точке, а его направление указывает на направление наискорейшего изменения.
Знание градиента функции позволяет эффективно настраивать параметры моделей, находить экстремумы функций и улучшать производительность алгоритмов оптимизации. Наши знания о градиенте функции и его применении имеют широкий спектр применений и играют важную роль в различных областях, связанных с математикой, программированием и алгоритмами.
Градиент
Как появляется перхоть? [Veritasium]
10. ФНП. Градиент и производная по направлению функции двух переменных.
Математика без Ху%!ни. Частные производные функции нескольких переменных. Градиент.
ГАЙД НА ISO VALORANT - ISO НЕ ІМБА!
[DeepLearning - видео 2] Градиентный спуск: как учатся нейронные сети
Лекция. Вычисление производной. Градиент