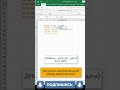
Что Такое Косинус В Произвольном Треугольнике

Косинус в произвольном треугольнике является тригонометрической функцией, которая определяется отношением длины прилежащего катета к гипотенузе треугольника. В случае произвольного треугольника, где угол alfa лежит напротив стороны a, косинус этого угла можно вычислить с помощью формулы: cos(alfa) = a / c, где c - длина гипотенузы треугольника.

Косинус в произвольном треугольнике имеет ряд интересных свойств. Например, он позволяет вычислить длину стороны треугольника по двум известным сторонам и углу между ними. Для этого можно использовать теорему косинусов, которая устанавливает следующую связь: a^2 = b^2 + c^2 - 2bc * cos(alfa), где a, b и c - длины сторон треугольника, а alfa - угол между сторонами a и b.

Также косинус в произвольном треугольнике является одним из основных элементов при решении треугольных задач. Он может быть использован, например, для нахождения углов треугольника, зная длины его сторон, или для определения площади треугольника по длинам его сторон и углу между ними. Кроме того, косинус в произвольном треугольнике играет важную роль в применении тригонометрии в различных областях, включая физику, инженерию и компьютерную графику.