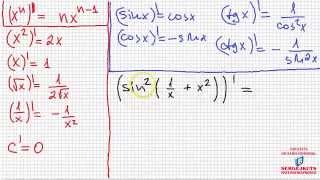КАК НАЙТИ КОЭФФИЦИЕНТ ЛИНЕЙНОЙ ФУНКЦИИ ПО ДВУМ ТОЧКАМ
Коэффициент линейной функции может быть найден по двум точкам на графике. Для этого нужно использовать формулу наклона прямой (коэффициент наклона), которая выражается разностью изменения значений y и x для этих точек.
Пусть (x1, y1) и (x2, y2) - это координаты двух точек. Тогда формула наклона будет выглядеть так:
Коэффициент наклона (k) = (y2 - y1)/ (x2 - x1)
Это выражение представляет отношение изменения значения y к изменению значения x между этими точками.
Найдя коэффициент наклона, мы можем записать уравнение прямой в виде y = kx + b, где b - это y-пересечение (значение y в точке пересечения с осью y).
Для нахождения коэффициента наклона к линейной функции по двум точкам, нужно знать координаты этих точек и применить формулу, описанную выше.
Линейная функция и ее график. 7 класс.
Функция. Практическая часть. 7 класс.
Уравнение прямой по двум точкам
Как составить уравнение прямой, проходящей через две точки на плоскости - Математика
Построить график ЛИНЕЙНОЙ функции и найти:
Составляем уравнение прямой по точкам
Математика без Ху%!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.
Линейная функция и ее график. Практическая часть. 7 класс.
ЛИНЕЙНАЯ ФУНКЦИЯ - БАЗА - Как составить из 2 точек уравнение функции?
Линейная функция: краткие ответы на важные вопросы - Математика - TutorOnline