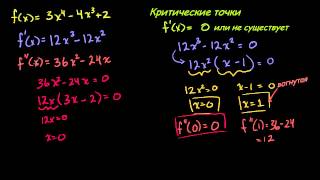КАК ИССЛЕДОВАТЬ ФУНКЦИЮ НА НЕПРЕРЫВНОСТЬ И ДИФФЕРЕНЦИРУЕМОСТЬ
Исследование функций на непрерывность и дифференцируемость является важным аспектом в математике и анализе. При изучении функций необходимо установить, непрерывна ли функция на заданном интервале, а также определить, является ли она дифференцируемой в заданной точке или на заданном интервале.
Для начала, рассмотрим понятие непрерывности функции. Функция является непрерывной в точке, если ее значение в этой точке равно пределу ее значений по мере приближения аргумента к данной точке. Для исследования непрерывности функции на заданном интервале можно применить теорему о непрерывности, которая устанавливает условия, при которых функция будет непрерывной на интервале.
Следующим шагом является анализ дифференцируемости функции. Функция является дифференцируемой в точке, если существует конечный предел приближения к данной точке, который определяет скорость изменения функции. Чтобы установить дифференцируемость функции в заданной точке или на интервале, необходимо проверить выполнение определенных условий, таких как существование конечного предела в этой точке и непрерывность функции в этой точке или на интервале.
Для выполнения исследования функции на непрерывность и дифференцируемость можно использовать различные методы и инструменты, такие как графический анализ, аналитические методы, а также теоремы и правила дифференцирования и непрерывности функций.
Важно отметить, что исследование функций на непрерывность и дифференцируемость позволяет нам лучше понять их поведение и свойства. Оно может быть полезно для решения различных задач в математике, физике, экономике и других областях, где функции играют важную роль.
✓Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин
Математика без Ху%!ни. Исследование функции, график. Первая, вторая производная, асимптоты.
Непрерывность функции и точки разрыва функции
0403.Связь дифференцируемости и непрерывности
Определение производной функции в точке. Непрерывность дифференцируемой функции. Билет 13
Математика без Ху%!ни. Непрерывность функции, точки разрыва.
Производная. Часть 5. Дифференцируемость и непрерывность функции. Несуществование производной.
✓ Непрерывность функции в точке. Непрерывность многочленов - матан #019 - Борис Трушин
Исследование функции на дифференцируемость (часть 1)
Математический анализ, 5 урок, Непрерывность функции