Как Исследовать Функцию На Дифференцируемость

Дифференцируемость функции – важное понятие в математическом анализе. Для исследования функции на дифференцируемость необходимо проверить выполнение определенных условий.

Во-первых, нужно убедиться, что функция определена на заданной области. Затем, необходимо проверить существование производной функции в каждой точке этой области. Если производная существует, то функция является дифференцируемой в этой точке.

Однако, наличие производной не гарантирует дифференцируемость функции на всей области. Для этого требуется проверить непрерывность производной на всей области определения функции.

Также, нельзя забывать о дифференцируемости функции на границе области определения. Для этого необходимо проверить существование односторонних производных в точках, граничащих с этой областью.

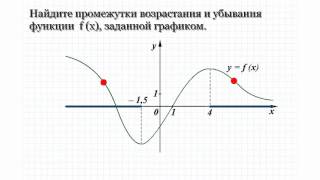
Для изучения функции на дифференцируемость можно использовать различные методы, такие как правила дифференцирования, изучение локальных экстремумов и поведение функции на различных интервалах.

Кроме того, нужно помнить, что функция может быть дифференцируемой на подмножестве своей области определения, поэтому для полного исследования функции на дифференцируемость необходимо проанализировать всю область определения.