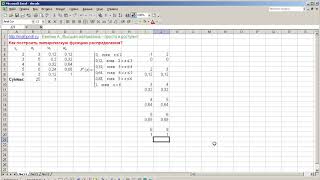
ГДЕ ПРОИЗВОДНАЯ ФУНКЦИИ ПРИНИМАЕТ НАИМЕНЬШЕЕ ЗНАЧЕНИЕ
Для того чтобы определить, где производная функции принимает наименьшее значение, необходимо проанализировать график этой функции и найти точки экстремума.
Точками экстремума функции, в данном случае наименьшего значения производной, считаются точки, в которых производная функции равна нулю или не существует. Существует несколько методов нахождения этих точек, включая производные высших порядков, метод Ферма, метод дифференцирования, метод градиентного спуска и другие.
После нахождения точек экстремума необходимо проанализировать значения производной на интервалах между этими точками. Если производная меняет знак на интервале, то это указывает на то, что производная принимает наименьшее значение в середине этого интервала.
Определение конкретных точек и интервалов, в которых производная функции принимает наименьшее значение, зависит от конкретной функции, ее формулы и ограничений. Необходимо рассмотреть каждый случай индивидуально и применить соответствующие методы анализа.
Наибольшее и наименьшее значение функции. 10 класс.
Понятие производной и предела I Простыми словами I 10/11 класс
НАИМЕНЬШЕ ЗНАЧЕНИЕ ФУНКЦИИ ПО ГРАФИКУ ПРОИЗВОДНОЙ ?📈 #математика #егэ #егэ2022 #производная
ЕГЭ-2022: задание №6. Наибольшее/наименьшее значение функции по производной
Задача 7 ЕГЭ по математике. Урок 15.
7 изображен график производной, в какой точке отрезка функция принимает наименьшее значение
Математический анализ, 13 урок, Наибольшее и наименьшее значение функции на отрезке
В какой точке отрезка функция принимает наименьшее значение