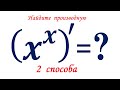ЧТО ТАКОЕ ПРОИЗВОДНАЯ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Производная функции одной переменной - это основной показатель изменения функции в зависимости от изменения ее аргумента. Фактически, производная показывает наклон касательной к графику функции в каждой точке. Она дает информацию о скорости изменения значения функции, ее росте или убывании.

Производную функции можно определить как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Если предел существует, то этот предел и является производной функции в данной точке.

Производная функции одной переменной имеет множество приложений в математике, физике, экономике и других областях. Зная производную функции, мы можем определить ее экстремумы (максимумы и минимумы), точки перегиба, установить характер изменений функции в различных интервалах и провести анализ ее поведения.

Существует несколько способов нахождения производной функции: использование аналитических методов, дифференциального исчисления и численных методов. При решении задач можно применять основные правила дифференцирования, такие как правило производной суммы, производной произведения, производной сложной функции и др. На практике также используются компьютерные программы для символьного или численного дифференцирования функций.

Важно отметить, что функция может иметь разные значения производной в различных точках. Это связано с изменением характера функции, наличием разрывов или других особенностей. Изучение производной функции помогает понять ее свойства и использовать эту информацию для решения различных задач и проблем, возникающих в различных областях науки и техники.

SQM 4/24: Halstead Complexity

Дифференциал функции

Производная: секретные методы решения. Готовимся к ЕГЭ - Математика TutorOnline

АЛГЕБРА С НУЛЯ — Что такое Производная?

Производная функции. 10 класс.

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.

Парадокс производной - Суть Матанализа, глава 2

✓ Производная. Начало - Ботай со мной #056 - Борис Трушин