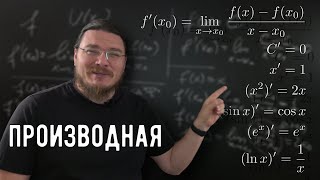КОГДА СХОДИТСЯ НЕСОБСТВЕННЫЙ ИНТЕГРАЛ 1 РОДА
Несобственный интеграл 1 рода является математическим понятием, которое обозначает интеграл от функции на бесконечном интервале или на интервале с бесконечным числом точек разрыва. Такой интеграл может сходиться или расходиться в зависимости от свойств функции.
Сходимость или расходимость несобственного интеграла 1 рода определяется с использованием критериев сходимости, таких как критерий сравнения, критерий интегрирования по частям и критерий Дирихле. Если для функции выполняются соответствующие условия, то интеграл сходится, иначе он расходится.
Критерий сравнения гласит, что если существует интегрируемая на данном отрезке функция, ограниченная сверху или снизу данной функцией, то интегралы от обеих функций сходятся или расходятся одновременно. При применении критерия сравнения необходимо выбрать подходящую функцию для сравнения с исходной.
Критерий интегрирования по частям основан на формуле интегрирования по частям. Если подынтегральная функция удовлетворяет определенным условиям, то этот критерий позволяет определить сходимость или расходимость интеграла, используя интеграл от производной функции.
Критерий Дирихле используется для определения сходимости или расходимости интеграла при наличии произведения двух функций. Если одна функция монотонно убывает до нуля, а интеграл от второй функции ограничен, то несобственный интеграл 1 рода сходится.
Таким образом, сходимость или расходимость несобственного интеграла 1 рода зависит от свойств подынтегральной функции и может быть определена с использованием различных критериев сходимости.
11. Признаки сходимости несобственных интегралов 1 рода. 2 признак сравнения.
9.1 Несобственные интегралы 1 рода примеры решения #1
Математика без ху%!ни. Несобственные интегралы, часть 1. Сходимость и расходимость.
12. Несобственные интегралы 1 рода от знакопеременных функций. Абсолютная сходимость интегралов.
9.2 Несобственный интеграл 1 рода примеры решения #2
Математический анализ, 26 урок, Несобственные интегралы
10. Признаки сходимости несобственных интегралов. Признак сравнения.
Математический анализ, 27 урок, Геометрическое приложение определенного интеграла