ЧТО ГЕОМЕТРИЧЕСКИ ПРЕДСТАВЛЯЕТ СОБОЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ

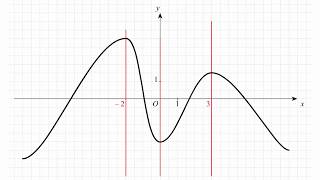
Дифференциал функции геометрически представляет собой приближенное линейное отображение в окрестности данной точки на графике функции. Он определяет касательную к кривой графика и позволяет описать изменение значения функции при малых изменениях аргумента.

Математически дифференциал функции f(x) определяется как произведение частной производной функции по аргументу на дифференциал аргумента dx:

df(x) = f'(x) * dx.

Геометрически дифференциал представляет собой прямую линию, касательную к графику функции вблизи данной точки. Эта линия имеет угол наклона, равный производной функции в этой точке.

Визуально дифференциал функции можно представить как невеликое приближение касательной, которая наилучшим образом аппроксимирует поведение функции вблизи данной точки. Приближение становится точнее, поскольку изменение значения функции становится меньше, когда изменение аргумента становится меньше.

Дифференциал функции имеет важное значение в дифференциальном исчислении, позволяя анализировать локальное поведение функций и использовать его в дальнейшем, например, для нахождения точек экстремума и оптимизации функций. Он также помогает понять графическую интерпретацию понятия производной.

Самый дикий параметр - Физтех-1994. Математика - Борис Трушин -

22. Дифференциал функции и его геометрический смысл

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.

21. Дифференциал функции

✓ Производная. Начало - Ботай со мной #056 - Борис Трушин

Интегралы№1 Понятие Дифференциала Функции