Как Найти Субдифференциал Функции

Субдифференциал функции - это математический объект, который позволяет оценить скорость изменения функции в точке. Он является обобщением понятия производной на случай, когда функция не обязательно дифференцируема.

Для нахождения субдифференциала функции существует несколько методов, включая геометрический и аналитический подходы.

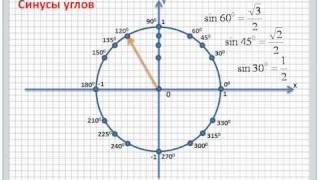
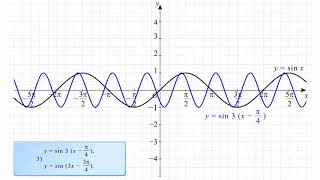
Один из способов построения субдифференциала - использование геометрического представления функции и ее графика. В этом случае субдифференциал функции определяется как множество наклонов касательных к графику функции в каждой точке. Такой подход позволяет наглядно представить субдифференциал и использовать его свойства для решения оптимизационных задач.

Аналитический подход основан на использовании свойств функции и ее производных. Субдифференциал функции может быть найден как множество всех значений градиента функции в заданной точке. Градиент является вектором, который показывает направление наибольшего возрастания функции в данной точке. Вычисление градиента функции требует знания ее частных производных, которые могут быть выражены через производные более простых функций.

В заключение, нахождение субдифференциала функции позволяет получить информацию о скорости изменения функции в каждой точке. Это полезный инструмент в оптимизации и анализе функций, особенно в случаях, когда функция не является дифференцируемой.