КАК ВЕДЕТ СЕБЯ ПРОИЗВОДНАЯ ПРИ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЯХ НАД ФУНКЦИЯМИ КРАТКО
Производная функции представляет собой показатель ее скорости изменения в каждой точке. При арифметических операциях над функциями производная также ведет себя определенным образом.
При сложении или вычитании двух функций, производная суммы или разности равна сумме или разности производных соответственно.
Если у нас есть функция f(x) и g(x), то производная их произведения равна произведению производной f(x) и g(x) сумме– произведения функции f(x) на производную g(x) и произведения функции g(x) на производную f(x).
При делении функций производная также имеет свои особенности. Если у нас есть функция f(x) и g(x), то производная частного равна разности произведения функции f(x) на производную g(x) и произведения функции g(x) на производную f(x) деленного на квадрат g(x).
Таким образом, производная функции при арифметических операциях определяется определенными правилами, что позволяет более эффективно работать с функциями и их производными.
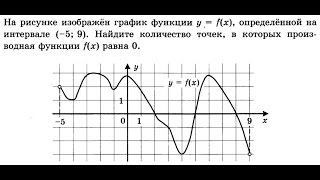
Производная функции по определению
Производная функции. 10 класс.
Производная в ЕГЭ. Вебинар - Математика
Производная: секретные методы решения. Готовимся к ЕГЭ - Математика TutorOnline
Понятие производной и предела I Простыми словами I 10/11 класс
✓ Определение производной. Производные основных функций - матан #030 - Борис Трушин