Когда Не Существует Обратной Функции

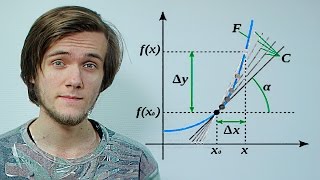
Когда мы говорим о функциях, часто предполагаем, что каждая функция имеет обратную функцию. Однако есть ситуации, когда обратная функция не существует. Пусть у нас есть функция f(x), которую мы хотим инвертировать. Вот несколько причин, по которым может не существовать обратной функции.

1. Неинъективная функция: Если функция f(x) является неинъективной, то есть существуют разные значения x, которые отображаются в одно и то же значение f(x), то обратная функция не может быть определена однозначно. Например, функция f(x) = x^2 не является инъективной, поэтому у нее нет обратной функции.

2. Недифференцируемая функция: Обратная функция обычно определяется на основе производной функции f(x). Однако, если функция f(x) не дифференцируема в некоторых точках или на интервале, то ее обратная функция может быть недифференцируемой. Например, функция знака (sign(x)) не имеет обратной функции в точке x = 0, так как она не дифференцируема в этой точке.

3. Невыпуклая функция: Если функция f(x) не является выпуклой, то ее обратная функция также может не существовать. Выпуклость функции связана с монотонностью ее производной, и если производная функции не удовлетворяет определенным условиям, то обратная функция не будет существовать. Например, функция f(x) = x^3 не является выпуклой, и у нее нет обратной функции.

4. Неограниченная функция: Если функция f(x) не ограничена сверху или снизу на заданном интервале, то ее обратная функция может быть определена только на части этого интервала. Например, функция f(x) = e^x не ограничена и не имеет обратной функции на всей числовой оси.

Выводящий пример для всех этих случаев является функция f(x) = x^2, которая не является инъективной, недифференцируемой, не выпуклой и неограниченной. В таких случаях отсутствует обратная функция, и это важно учитывать при анализе и решении математических и инженерных задач.