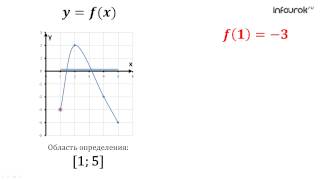Как Исследовать Поведение Функции В Точке

Когда мы хотим исследовать поведение функции в определенной точке, становится важным понять, как функция проявляет себя рядом с этой точкой. Существует несколько основных аспектов, которые мы можем рассмотреть, чтобы полностью понять функцию в данной точке.

Первый аспект - это значение функции в самой точке. Для этого подставляем координаты точки в уравнение функции и находим значение. Это помогает нам понять, в какой позиции находится функция относительно оси y в данной точке.

Второй аспект, который мы можем рассмотреть, - это производная функции в этой точке. Производная функции показывает нам скорость изменения функции в данной точке. Если производная равна нулю, то это может указывать на экстремумы - минимумы или максимумы функции в этой точке.

Третий аспект - это пределы функции в окрестности данной точки. Пределы позволяют нам увидеть, как функция ведет себя при приближении к данной точке. Узнавая пределы функции, мы можем определить такие вещи, как асимптоты или разрывы функции.

Четвертый аспект - это поведение функции в окрестности данной точки. Рассматривая значения функции вблизи данной точки, мы можем обнаружить такие вещи, как монотонность (возрастание или убывание) или выпуклость функции в этой области.

Исследование поведения функции в точке - это важный этап в изучении математических функций. Понимание всех вышеперечисленных аспектов поможет нам получить полное представление о функции в данной точке и использовать эту информацию для дальнейших математических и программных расчетов.