КАК ЗАПИСАТЬ ВСЮ СОВОКУПНОСТЬ ПЕРВООБРАЗНЫХ ФУНКЦИЙ
Чтобы записать всю совокупность первообразных функций, необходимо использовать интегральное исчисление. Первообразная функция является обратной операцией к производной и позволяет найти функцию, производная которой равна данной функции.
Для записи первообразной функции необходимо использовать интегральный знак ∫, за которым указывается функция, для которой ищется первообразная, а также дифференциальная переменная. Интеграл представляет собой неопределенный вариант первообразной функции, и решение может содержать постоянную C, называемую постоянной интегрирования.
Пример записи первообразной функции: ∫f(x) dx. Здесь f(x) - функция, для которой ищется первообразная, а dx - дифференциальная переменная. После нахождения первообразной функции получаем выражение, например, F(x) + C, где F(x) - первообразная функция, а C - постоянная интегрирования.
Для более сложных функций существуют различные методы вычисления первообразных, такие как метод замены переменной, метод интегрирования по частям и т.д. Эти методы позволяют находить первообразные функции различных типов и структур.
Использование первообразных функций является важным инструментом в математике, физике, инженерии и других областях науки. Они позволяют решать задачи, связанные с определением площадей, объемов, скоростей изменения и многих других величин.
Первообразная. Практическая часть. 11 класс.
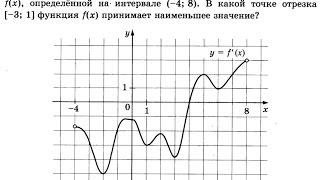
ЗАДАНИЕ №7 Производная и графики функции - PARTA
Что такое первообразная функции
Первообразная. 11 класс.
Первообразная функции, проходящая через точку
Первообразная. Практическая часть. 11 класс.
11 класс, 7 урок, Преобразование выражений содержащих радикалы