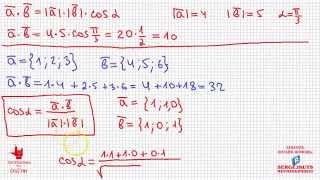Как Выразить Косинус Через Синус По Формулам Приведения И Сравнить Числа

Косинус и синус являются основными тригонометрическими функциями, которые тесно связаны между собой. Существуют формулы приведения, которые позволяют выразить косинус через синус и наоборот.

Формула приведения для косинуса гласит:

cos(α) = sin(π/2 - α)

Аналогично, для выражения синуса через косинус:

sin(α) = cos(π/2 - α)

Таким образом, чтобы выразить косинус через синус, необходимо вычислить синус от дополнения угла до 90°. А чтобы выразить синус через косинус, нужно вычислить косинус от того же дополнения угла.

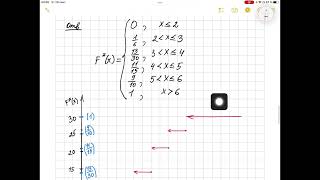
Числа, которые получаются в результате вычислений, могут быть сравнены для проверки точности и связи между собой. На практике, если угол α задан в радианах, то значения косинуса и синуса должны быть равны в пределах некоторой погрешности, обусловленной округлением и неточностью вычислений. В случае отклонений от равенства косинуса и синуса, возможно, потребуется проверить правильность примененных формул и точность вычислений.