КАК ПОНЯТЬ ЧТО ФУНКЦИЯ СИММЕТРИЧНА ОТНОСИТЕЛЬНО НАЧАЛА КООРДИНАТ

Чтобы понять, является ли функция симметричной относительно начала координат, необходимо проверить выполнение двух условий.

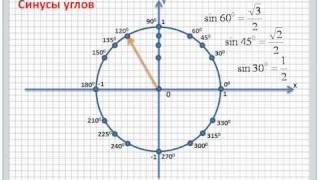
Первое условие заключается в том, что функция должна быть четной. Это означает, что для любого значения x, значение функции для -x будет равно значению функции для x. Если это условие выполняется, то функция обладает осевой симметрией относительно оси OY.

Второе условие заключается в том, что функция должна проходить через начало координат (0,0). Это означает, что значение функции для x=0 должно быть равно 0. Если оба условия выполняются, то функция симметрична относительно начала координат.

Для проверки четности функции можно заменить переменную x на -x в выражении функции и сравнить полученное выражение с изначальным. Если они равны, то функция является четной. Если функция проходит через начало координат, тогда значение функции при x=0 будет равно 0.

Используя эти два условия, можно определить, является ли функция симметричной относительно начала координат или нет.

Матан за час. Шпаргалка для первокурсника. Высшая математика

Точки пересечения графика линейной функции с координатными осями. 7 класс.

Четные и нечетные функции

Реакция на результаты ЕГЭ 2022 по русскому языку

Как найти точку, симметричную точке А(3;4) относительно начала координат. Как решать. Простой способ

Примеры использования функции ДВССЫЛ (INDIRECT)