Как Выразить Через Тригонометрические Функции Углов Альфа И Бета Отрезки

Чтобы выразить отрезки через тригонометрические функции углов альфа и бета, необходимо использовать соотношения тригонометрии и тригонометрические формулы.

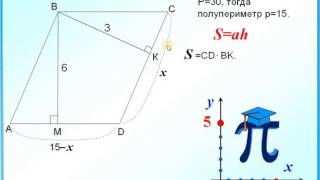
Например, для выражения отрезка AB через углы альфа и бета можно использовать формулу синуса. Если известны длины отрезков AC и BC, а также значения углов альфа и бета, то отрезок AB можно найти следующим образом:

AB = √(AC² + BC² - 2·AC·BC·cos(α - β))

В данной формуле cos(α - β) - это косинус разности углов альфа и бета, который может быть выражен через другие тригонометрические функции и тригонометрические тождества.

Если углы альфа и бета выражены через синусы и косинусы других углов, то полезными могут оказаться формулы сложения и вычитания тригонометрических функций, которые позволяют выразить сумму и разность синусов и косинусов через произведение и частное тригонометрических функций.

Также, для выражения отрезков через углы альфа и бета можно использовать формулу тангенса для треугольников. Если известны значения углов альфа и бета, а также длины сторон треугольника, то можно выразить отрезки через тангенсы углов:

AB = BC·tg(α) + AC·tg(β)

Данные формулы являются лишь некоторыми примерами того, как можно выразить отрезки через тригонометрические функции углов альфа и бета. В зависимости от конкретной задачи или контекста, могут использоваться и другие формулы и соотношения.