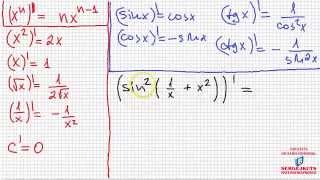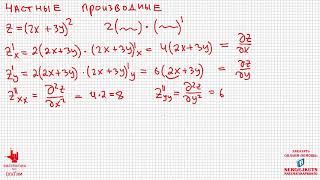КАК НАЙТИ ПРОМЕЖУТКИ МОНОТОННОСТИ КВАДРАТИЧНОЙ ФУНКЦИИ

Промежутки монотонности квадратичной функции можно найти, проанализировав ее график. Квадратичная функция представляется уравнением вида f(x) = ax^2 + bx + c, где a, b и c - коэффициенты. Для определения промежутков монотонности необходимо рассмотреть знак производной функции.

Для начала, найдем производную функции f'(x) = 2ax + b. Затем проанализируем знак производной на интервалах, где она определена. Если производная положительна на интервале, то функция возрастает на этом интервале. Если производная отрицательна, то функция убывает. Промежутки монотонности квадратичной функции будут задаваться интервалами, на которых производная не меняет знака.

При анализе знака производной можно использовать также вершины параболы, которые можно найти по формуле x = -b / (2a). Если a положительно, то вершина будет являться точкой минимума, а если a отрицательно, то вершиной будет точка максимума.

Получив промежутки монотонности квадратичной функции, можно использовать эту информацию для построения графика, а также для анализа поведения функции на разных интервалах.

Промежутки монотонности

Урок 101. Монотонность, промежутки знакопостоянства квадратичной функции (8 класс)

Свойства функции. Промежутки возрастания и убывания функции. 10 класс.

Функция. Множество значений функции. Практическая часть. 10 класс.

СВОЙСТВА ФУНКЦИИ — Промежутки Знакопостоянства и Монотонности

Промежутки монотонности функции.

Вариант 29, № 7. Промежутки знакопостоянства квадратичной функции у=ax²+bx+c. Пример 1

Свойства функции. Промежутки знакопостоянства. 10 класс.

Исследование квадратичной функции. 8 класс.

ТЕПЕРЬ ТЫ ЛЕГКО ПОЙМЕШЬ свойства квадратичной функции — Парабола