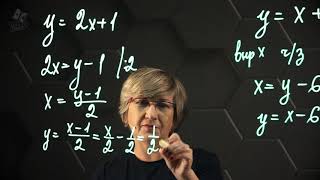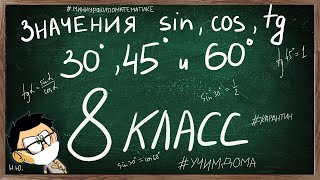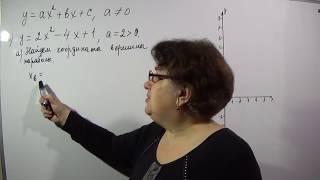Как Упрощать Выражения С Косинусами И Синусами

Косинусы и синусы являются основными тригонометрическими функциями, которые широко используются в математике, программировании и алгоритмах. Упрощение выражений с косинусами и синусами является важным навыком при решении различных задач.

Для упрощения выражений с косинусами и синусами можно применять различные тригонометрические тождества и свойства. Одним из ключевых тождеств является тригонометрическое тождество Эйлера, которое позволяет выразить косинус и синус через экспоненту:

$$e^{ix} = \cos(x) + i\sin(x)$$

Используя это тождество, можно заменять косинусы и синусы на экспоненты и сокращать выражения с помощью алгебраических операций. Например, выражение $$\cos^2(x) + \sin^2(x)$$ упрощается до $$1$$ с помощью тождества Эйлера.

Кроме того, существуют другие тригонометрические тождества, такие как тригонометрическая формула сложения и удвоения, которые могут быть полезны при упрощении выражений с косинусами и синусами.

При решении конкретных задач, например, при нахождении производных выражений с косинусами и синусами, можно использовать правила дифференцирования, такие как правило дифференцирования произведения и правило дифференцирования сложной функции.

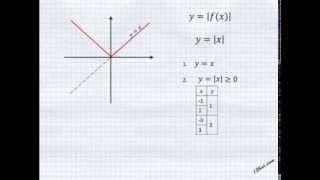
В общем случае, упрощение выражений с косинусами и синусами требует знания тригонометрических тождеств и алгебраических операций, а также понимания целей и контекста, в котором проводится упрощение.